Disclaimer
Die hier bereitgestellten Informationen stellen keine Finanzberatung dar und sind nicht als solche gedacht. Vielmehr sollen hier ein mathematisches Modell aufgestellt und die Wirkung der Änderung der Eingangsparameter aus reiner naturwissenschaftlicher Neugierde heraus analysiert werden. Sollten Sie Finanzberatung in Anspruch nehmen wollen, empfehlen wir Ihnen den Rat von einem qualifizierten Finanzberater (der wir nicht sind) einholen.
Einflüsse auf die Kredittilgung
Wie wir in dem Artikel „Den jährlichen effektiven Zinssatz aus dem nominalen Zinssatz berechnen“ gefunden haben, haben drei Größen einen wesentlichen Einfluss auf die Höhe und somit auch auf die Tilgung von Krediten:
- Die Kreditsumme s0,
- der nominale Zinssatz p und
- die monatliche Rate r.
Dann ergibt sich nach einem Monat (ohne Tilgung) folgende zurückzuzahlende Kreditsumme
$$s_1 = s_0 \cdot \left( \frac{p}{12} + 1 \right) – r .$$
Diese Formel beinhaltet die monatliche Zinslast z, die durch
$$z = \frac{p}{12}\cdot s_0$$
gegeben ist.
Außerdem kann man aus der Formel für s1 direkt einen Grenzfall ableiten. Wenn s1 = s0 ist, dann geht die gesamte monatliche Rate allein für die Deckung der Zinslast drauf. Das heißt, die nach Zahlung der monatlichen Rate ausstehende Kreditsumme hat sich nicht verändert. Das bedeutet, dass die monatliche Zinslast auch gleichzeitig die Geldrate ist, bei der die Kreditsumme gerade noch nicht anwächst. Liegt die monatliche Rate also unter z, steigt die noch ausstehende Kreditsumme an. Das sollte natürlich vermieden werden.
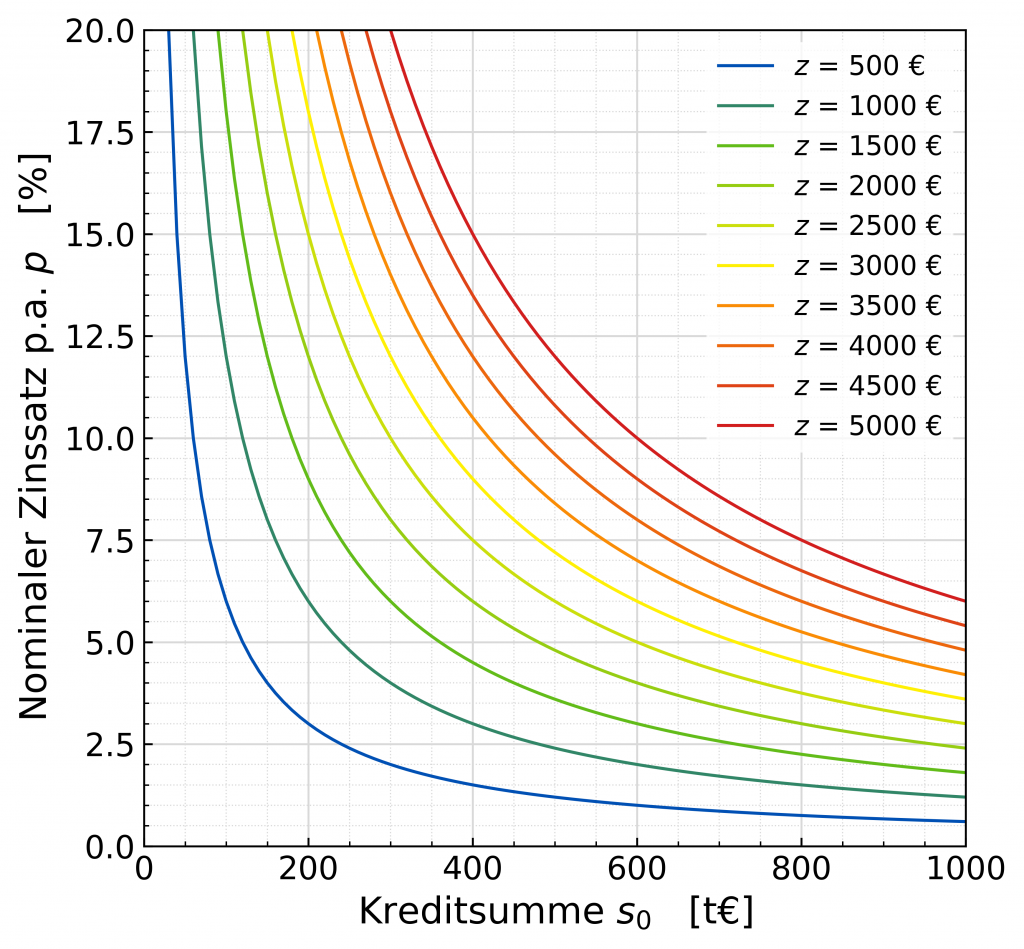
Die Grenzrate, bzw. die monatliche Zinslast z hängt also von zwei Parametern ab. Wir können nun fixe Werte der monatlichen Zinslast z vorgeben, und uns ansehen, welche Kombinationen des nominalen Zinssatzes p.a. p und der Anfangskreditsumme s0 hier zu finden sind. Dazu einmal kurz umgestellt
$$p = 12 \cdot \frac{z}{s_0}$$
und geplottet, ergibt folgende Abbildung.
Wie man diesen Graphen am besten liest
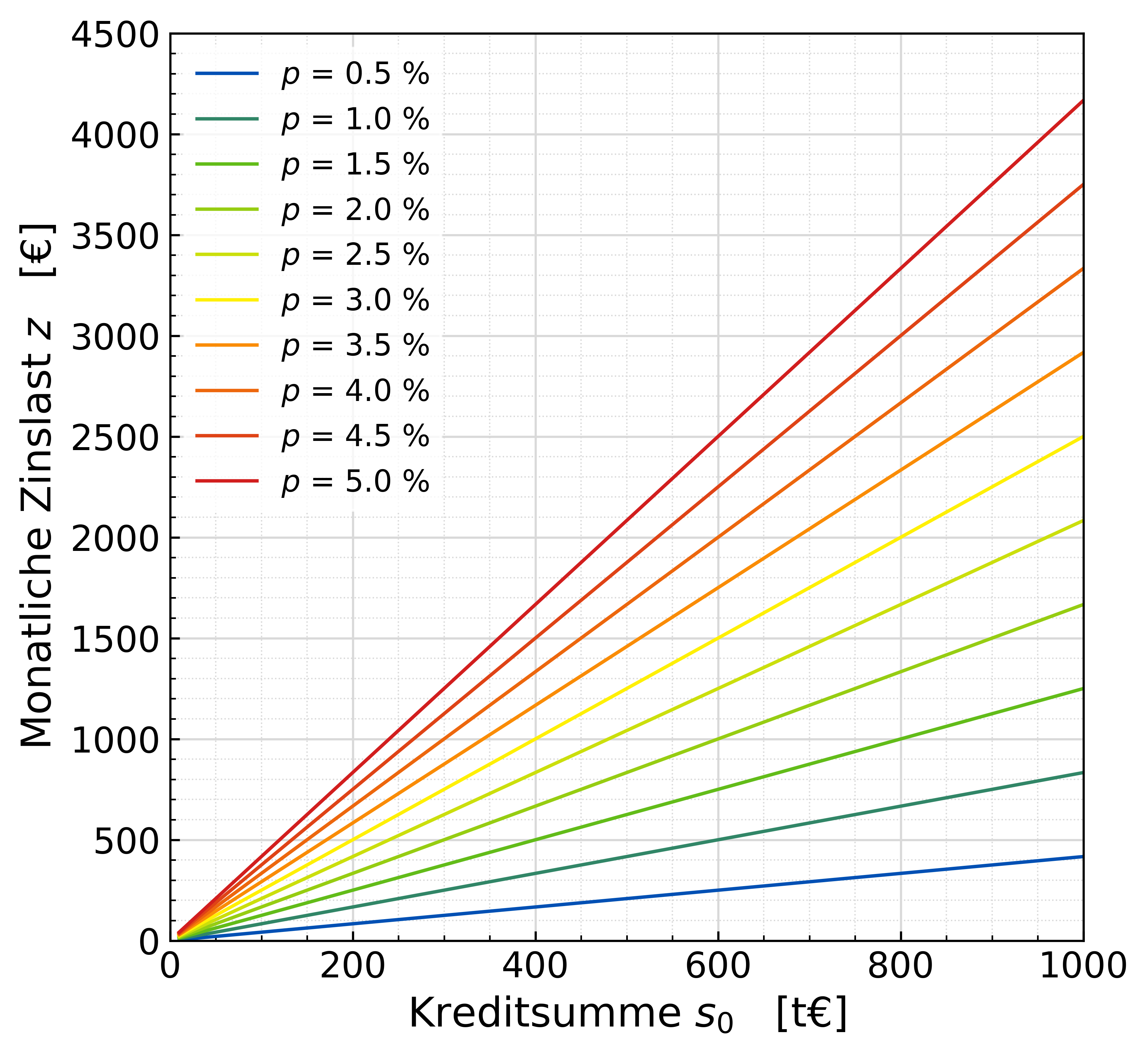
Angenommen, ein aktueller Zinssatz liegt bei 3,0 % und die Kreditsumme ist 600.000 €, dann ist die monatliche Zinslast 1.500,00 €. Wenn der Zinssatz sinkt, bleibt die Zinslast gleich, wenn eine höhere Kreditsumme finanziert wird. Daraus ergibt sich der geschwungene Verlauf der Kurzen in diesem Graphen.
Praktisch bedeutet das, wenn man eine monatliche Rate von 1.500,00 € stemmen kann, und die Zinsen bei 3,0 % liegen, kann man auf keinen Fall eine Kreditsumme finanzieren, die 600.000,00 € oder größer ist. Am besten sollte die Kreditsumme deutlich unter diesem Wert liegen, damit auch ein hoher Anteil der monatlichen Rate für die Tilgung der Kreditsumme aufgewendet werden kann, anstatt nur die Zinslast zu begleichen. Nur dann wird man in absehbarer Zeit das Darlehen begleichen können.
Anwenderfreundlichere Darstellung?
In der obigen Abbildung befinden sich die beiden externen Größen nominaler Zinssatz und Kreditsumme auf der x- und y-Achse und die Kurven ergeben sich aus dem Betrag, den man bereit ist monatlich für die Ratenzahlung zu leisten. Auch wenn die resultierenden Kurven aufgrund ihrer geschwungenen Form schön sind anzusehen, kann man versuchen, die Abbildung etwas zu optimieren und für den Anwender nutzbarer und somit freundlicher zu gestalten.
Man kann dies erreichen, wenn man die Perspektive etwas ändert, in dem man sagt, dass die monatliche Rate als auch die Kreditsumme von einem selbst frei gewählt werden können. Das bedeutet auch, dass man akzeptiert, nicht alle Kreditsummen finanzieren zu können. In diesem Fall wandern die monatliche Zinslast z, bzw. Rate, auf die y-Achse und die Kreditsumme s0 bleibt auf der x-Achse. Dann steigt die monatliche Rate linear mit der Kreditsumme an; je höher der Zinssatz p ist, desto steiler ist der Anstieg, und desto teurer wird die Kreditfinanzierung.
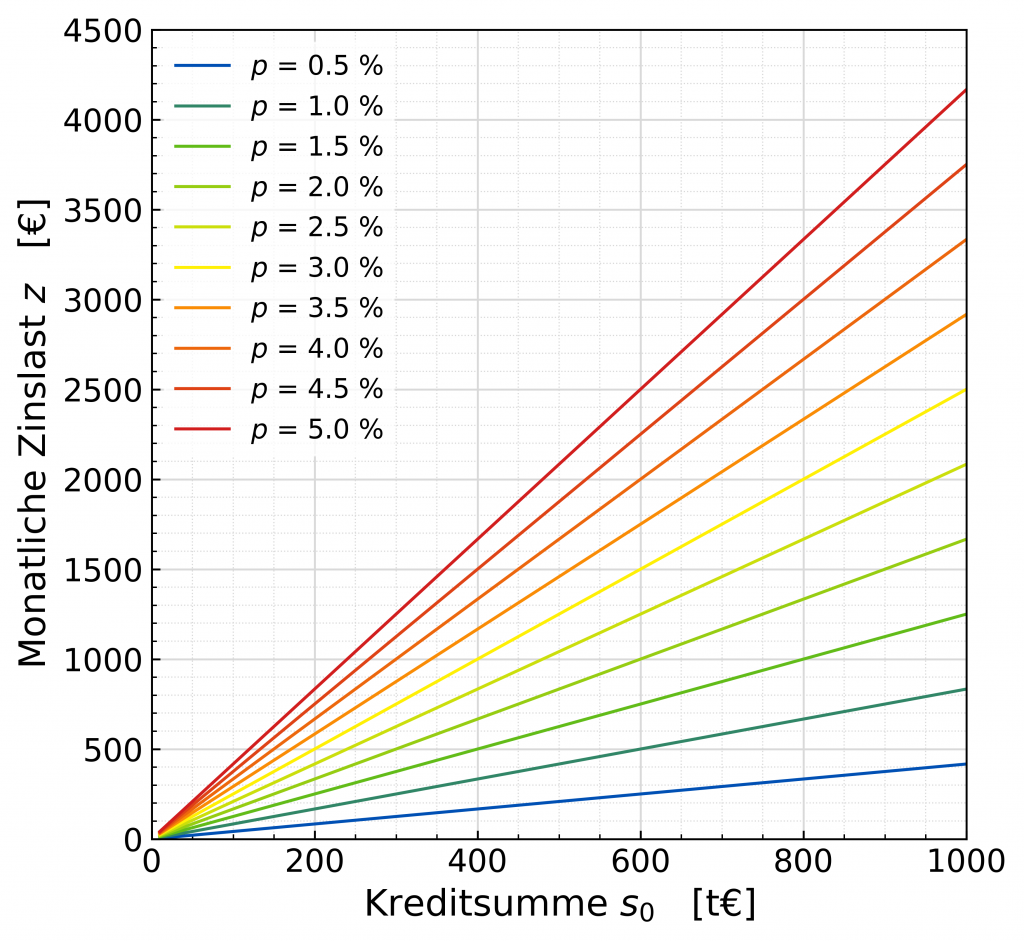
Der Vorteil in dieser Darstellung ist, dass man nun leicht von Größen realer Objekte auf die monatliche Zinslast schließen kann. Angenommen, die Kreditsumme würde 600.000 € betragen, und der nominale Zinssatz wäre 3,0 % (gelbe Linie), dann würden für die monatliche Zinslast 1.500 € fällig werden. Bei 3,5 % (erste orange Linie) wären das dann 1.750 € und bei 1,5 % (satt-grüne Linie) nur 750 €. In dieser Abbildung kann man also schnell die monatliche Zinslast bei Veränderung des nominalen Zinssatzes ablesen.
Gibt es eine Verbindung der monatlichen Zinslast zur Miete?
Uns ist bei der Recherche zu den monatlichen Zinslasten eine grobe Peilregel aufgefallen: Mit der monatlichen Zinslast könnte man sich eine Obergrenze für die Höhe der Mieten überlegen. Denn, wenn die monatliche Miete die Zinslast auf eine Immobilie übersteigt, fängt es für den Mieter an, sich eher zu lohnen, eine Immobilie zu kaufen und finanzieren, als eine Immobilie zu mieten. Beispiel: Hat eine Immobilie einen Wert von 400.000 €, und liegt der nominale Zinssatz p.a. bei 3,5 %, würden monatlich 1.166,67 € Zinslast anfallen. Kann man es sich leisten, noch ein paar Euro für die Kredittilgung draufzulegen, kann man also eine solche Immobilie auch erwerben, statt mieten. Die Immobilie würde dann zu Eigentum, während der Mieter nach auch nach Jahren keinen Besitz aufgebaut hat. Der hier ermittelte Zinslast ist momentan tatsächlich der Wert, den wir oft für ein Einfamilienhaus zur Miete gefunden haben. Dennoch gibt es bei der Finanzierung von Krediten einige Details und Tücken, die noch beachtet werden sollten (auch hier wieder der Hinweis, dass das hier keine Finanzberatung ist, sondern lediglich Schlussfolgerungen aus dem oben besprochenen drei-Parameter-Problem sind).