Den jährlichen effektiven Zinssatz aus dem nominalen Zinssatz berechnen

Disclaimer

Damit wir uns direkt richtig verstehen und keine Missverständnisse auftreten: Die hier bereitgestellten Informationen stellen keine Finanzberatung dar und sind nicht als solche gedacht. Vielmehr sollen hier ein mathematisches Modell aufgestellt und die Wirkung der Änderung der Eingangsparameter aus reiner naturwissenschaftlicher Neugierde heraus analysiert werden. Sollten Sie Finanzberatung in Anspruch nehmen wollen, empfehlen wie Ihnen den Rat von einem qualifizierten Finanzberater (der wir nicht sind) einholen.

Hintergrund und Fragestellung

Ich möchte verstehen, unter welchen Modalitäten welche Darlehenssumme möglich ist und welche Faktoren welchen Einfluss auf diese haben, um im Endeffekt nach einer geeigneten Immobilie suchen zu können. Wie oben schon gesagt, bin ich bin ich kein Finanzberater oder ähnliches, aber ich bin in der Lage mit ein paar Inputinformationen den Einfluss von verschiedenen Parametern in einem mathematischen System zu erforschen und zu analysieren. Und genau das möchte ich in diesem Artikel tun, und sehen, wie weit ich als Laie mit gesundem Menschenverstand das Themengebiet nachvollziehen kann. Um die Einflüsse auf einen Kredit analysieren zu können, muss ich aber wissen, welches die Einflussfaktoren auf die Kreditsumme und -rückzahlung sind.

Wichtige Parameter

Bei der Kreditfinanzierung von Immobilien gibt es immer eine Kreditsumme, die man selbst nicht besitzt und von der Bank geliehen bekommen will, um einen Hauskauf o.Ä. zu tätigen. Ist diese hoch, muss man viele Raten zahlen, was in der Konsequenz die Zeit zur Kredittilgung in die Höhe treibt. Ist die monatliche Ratenzahlung hoch, kann man die Tilgungszeit reduzieren. Außerdem gibt es noch den Zinssatz, mit dem die ausstehende Kreditsumme belastet wird. Ist der Zinssatz hoch, fließt mehr Geld der monatlichen Rate in die Tilgung der aufgelaufenen Zinslast und weniger Geld in die tatsächliche Tilgung der Darlehenssumme. Das bedeutet, wir haben bereits die wichtigsten Einflussfaktoren identifiziert:

1. Der Zinssatz p.a. (also pro Jahr),
2. die monatliche Rate an den Kreditgeber (Tilgung und Zinszahlung zusammen) und
3. die Darlehenssumme.

Der Zinssatz wird durch die Bank vorgegeben, schwankt aber mit der Zeit, von Monat zu Monat und von Jahr zu Jahr. Die monatliche Rate in Zusammenhang mit der Kreditsumme und der Darlehenshöhe bestimmen die Zeit, die benötigt wird, um das Geld zurückzuzahlen.

In diesem Artikel soll es zuerst um den Zinssatz gehen und darum, welchen Einfluss er hat sowie wie er für mich als Kreditnehmer am günstigsten liegen würde.

Der Zinssatz

Oft wird der nominale Zinssatz mit „p.a.“, das heißt pro Jahr, angegeben. Im Gegensatz dazu wird aber oft eine monatliche Rate zur Rückzahlung vereinbart. Das bedeutet, das auch die Zinslast pro Monat bestimmt werden muss. Aber wir kommt man von einem Zinssatz pro Jahr auf einen Zinssatz pro Monat? Und welche Folgen ergeben sich dann auf das gesamte Jahr gesehen?

Um vom Zinssatz pro Jahr (p.a.) p auf den monatlichen Zinssatz zu kommen, muss dieser einfach durch 12 Monate/Jahr dividiert werden. Das bedeutet, dass die eine Kreditsumme s = s₀ nach einer Zeit von einem Monat auf s₁ angestiegen ist

$$s_1 = \left( 1+\frac{p}{12} \right)\cdot s_0.$$

Nach einem weiteren Monat ergibt sich eine Kreditsumme

$$ s_2 = \left(1+\frac{p}{12}\right)\cdot s_1 = \left( 1 + \frac{p}{12} \right)^2\cdot s_0.$$

Verallgemeinert bedeutet das, dass nach einer Laufzeit von i Monaten, die aktuelle Kreditsumme gegeben werden kann durch

$$s_i = \left( 1+\frac{p}{12} \right)^i\cdot s_0,$$

vorausgesetzt keine Tilgungszahlungen wurden geleistet. In diesem Fall ist die Kreditsumme nach 12 Monaten also auf das (1+p/12)¹²-fache angestiegen. Daraus lässt sich der effektive Jahreszins p_eff bestimmen zu

$$p_{eff} = \frac{s_{12}}{s_0} – 1 = \left(1 + \frac{p}{12}\right)^{12} – 1.$$

Okay, aber um wieviel größer ist jetzt der effektive zum nominalen Jahreszinssatz? Dazu könnte man den Quotienten p_eff/p berechnen und mathematisch analysieren. Leider gibt es keinen einfachen analytischen Ausdruck, aber man kann sich mit einer „Hau-Drauf“-Methode behelfen, indem man einfach ein paar schöne Plots anstellt, denn ein Bild (also hier ein Plot) sagt bekanntlich mehr als tausend Worte (oder mathematische Umformungen).

Plots zum Zusammenspiel von p_eff und p

Um schöne Plots zu erstellen, können wir in Python zuerst eine Funktion definieren, die uns p_eff berechnet.

def f_peff(p, i = 12, m = 12):
	peff = (1 + p/m)**i - 1
	return peffCode-Sprache: JavaScript (javascript)

Und dann zum testen mit einem nominalen Zins von 4 % = 0,04

f_peff(0.04)Code-Sprache: CSS (css)

erzählt man 4,07 % als effektiver Jahreszins.

Hier kann man gut erkennen, dass der effektive Jahreszins größer ist, als der nominale Jahreszins (p.a.). Und anhand der Formel kann man erkennen, dass der effektive vom nominalen Jahreszins abhängt.

Für ein Array von p von 0 bis 10 % können wir nun p_eff errechnen und es als Funktion, das heißt in Abhängigkeit von p auftragen.

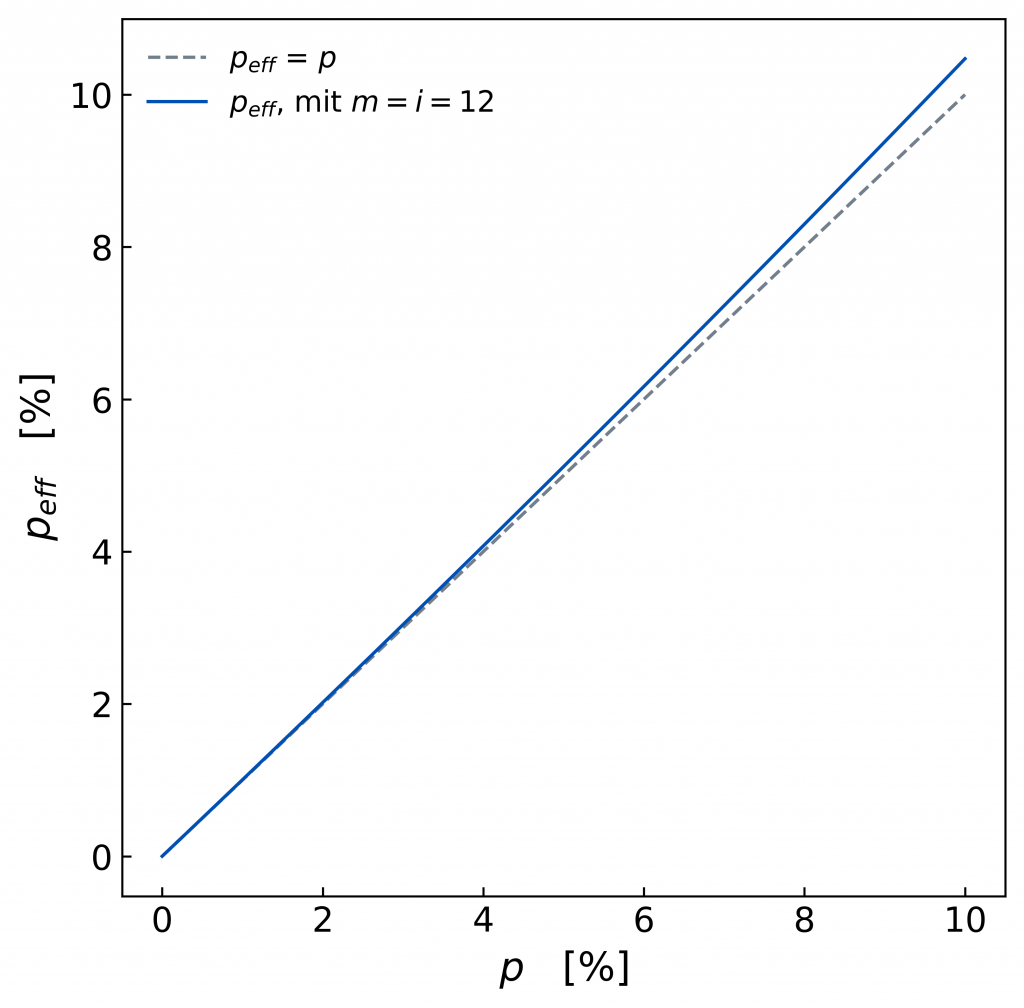
Da die blaue Linie von p_eff über der grau-gestrichelten Linie von p liegt, weiß man dass der effektive Jahreszinssatz höher liegt als der nominale Jahreszinssatz, außer bei p = 0, da hier auch p_eff = 0. Das bedeutet aber auch, dass man im Hinterkopf haben sollte, dass die tatsächliche Zinsbelastung gegen durch den effektiven Zinssatz p_eff höher ist, als mit dem nominalen Jahreszins (p.a.) p angegeben. Diesen Unterschied kann man durch Abziehen von p von p_eff deutlich machen.

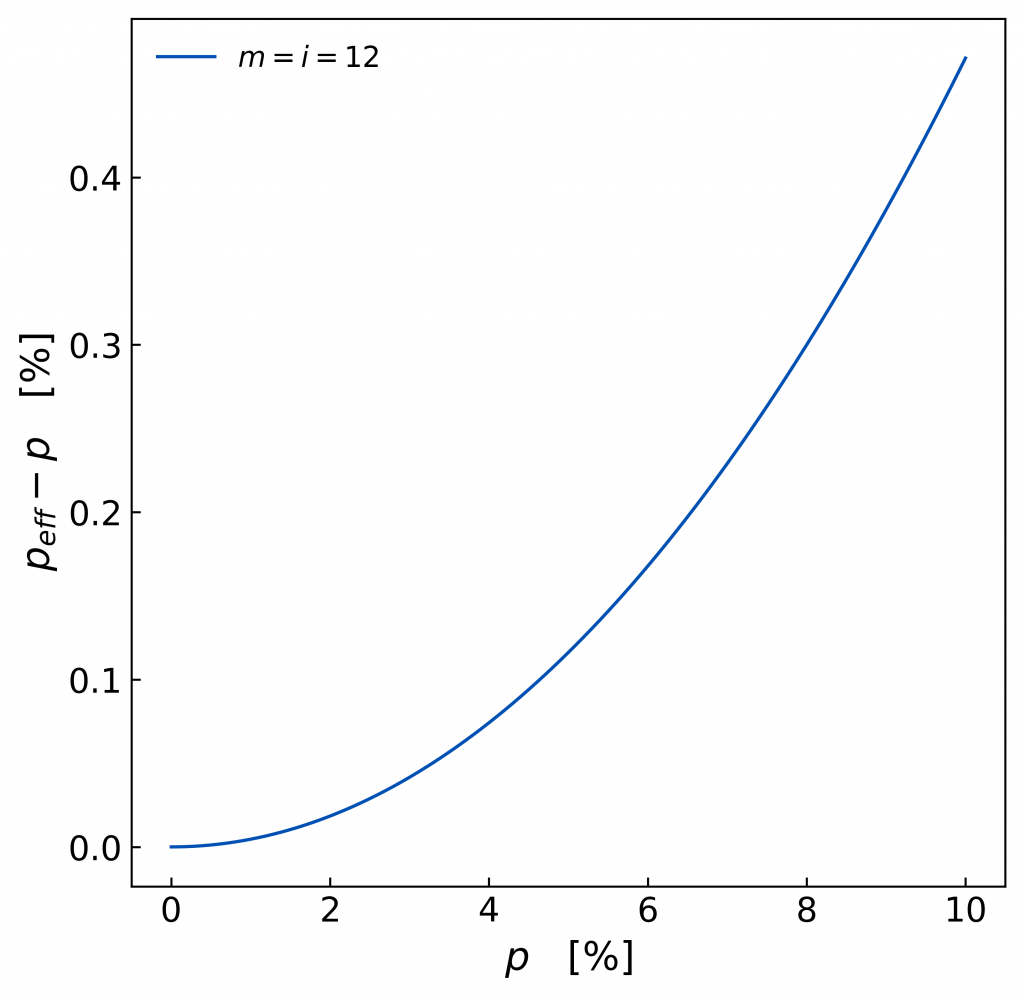
An der Ordinatenachse (y-Achse) kann man den Unterschied zwischen dem effektiven Jahreszinssatz p_eff und dem nominalen p ablesen. Zum Beispiel liegt p_eff bei p = 4 % in etwa 0,07 % über p, also bei 4,07 %.

Wer jetzt in Versuchung kommt, Werte von 0,07 % zu vernachlässigen, weil sie zu klein sind, sollte vielleicht ausprobieren, diese in Relation zu den Werten von p zu sehen. In diesem Fall ist nämlich p_eff 1,75 % größer als p. Natürlich kann man diesen relativen Unterschied zu p auch graphisch darstellen.

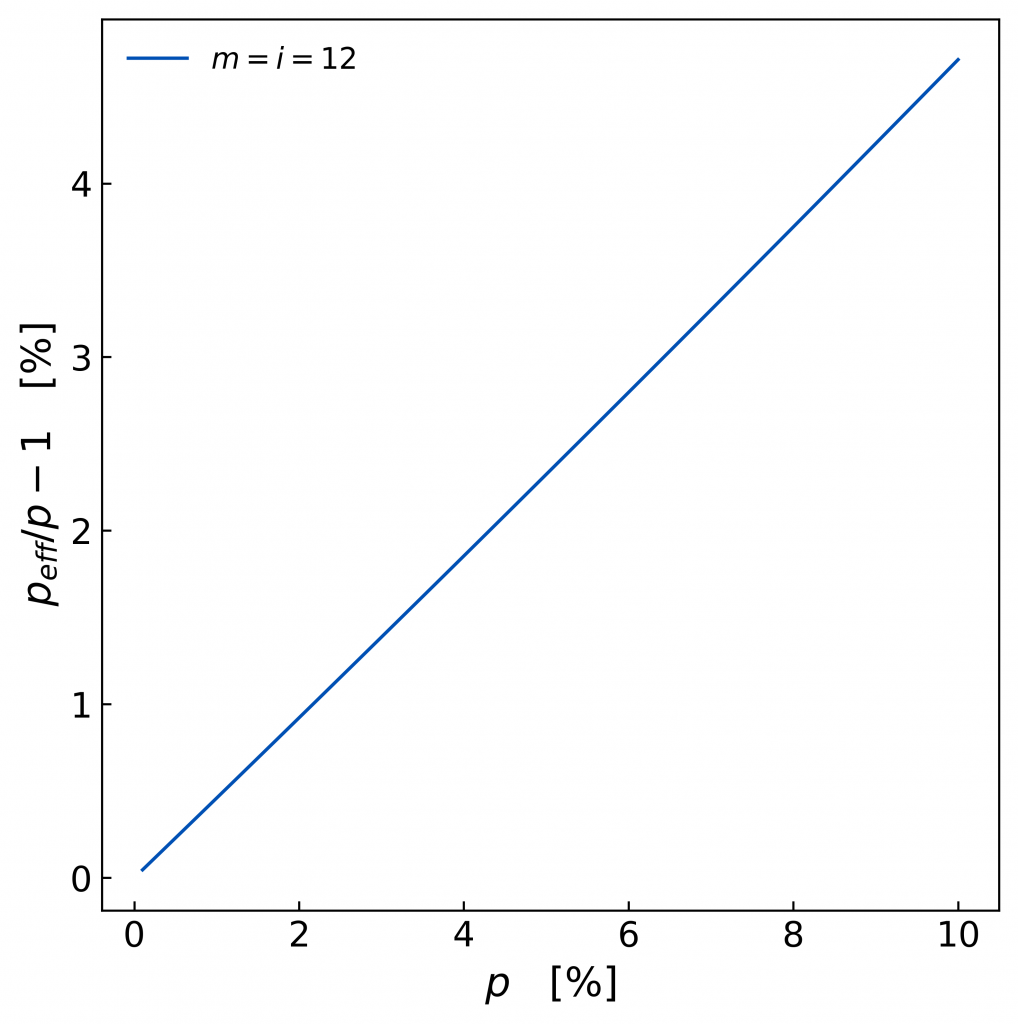
Mit dieser Grafik kann man schnell die Höhe des effektiven Jahreszinssatzes p_eff in Abhängigkeit des nominalten Zinssatzes (p.a.) p ermitteln: Bei p = 6 % kann man 2,8 % in der obigen Abbildung von p_eff/p – 1 ablesen. Das bedeutet, dass p_eff um 2,8 % größer ist als p. Also ist p_eff dann 6 % mal 1,028 = 6,17 %.

Einfluss der Ratenfrequenz

Bisher haben wir den effektiven Jahreszinssatz bei einer Ratenfrequenz von 12 Mal pro Jahr, also einer Teilung für jeden Monat, betrachtet. Natürlich kann man das Jahr beliebig oft teilen, zum Beispiel in 52 Wochen oder in 365 Tage. Welchen Einfluss hat diese Ratenrückzahlfrequenz auf p_eff? Macht es nur kaum einen Unterschied oder kann man heil froh sein, dass die Bank die Zahlungen nicht in kürzeren Abständen verlangt? Diese Frage soll mit der nächsten Abbildung geklärt werden.

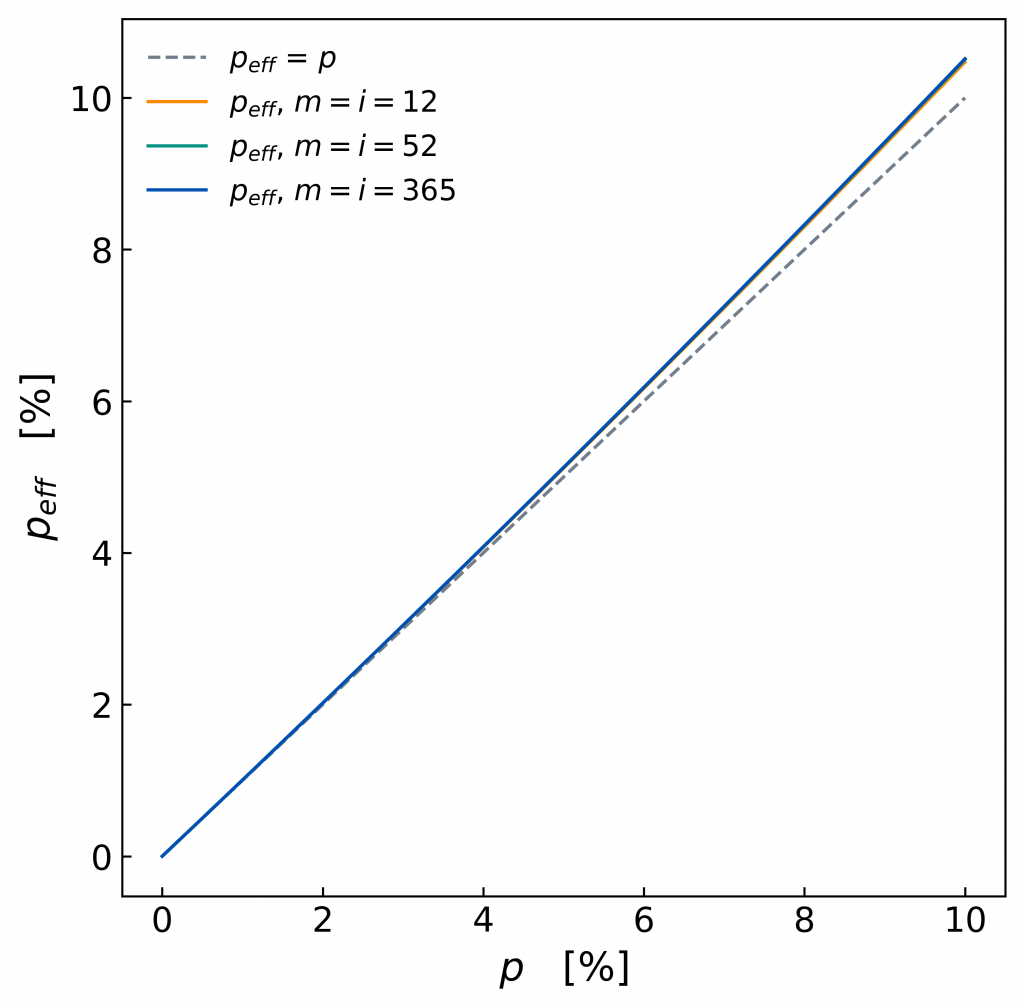
In orange ist die Berechnung wie oben gezeigt (= 12/Jahr), die grüne für eine Ratenfrequenz von 52/Jahr und die blaue Linie für eine Frequenz für 365/Jahr. Die beiden letzteren liegen über der Orangenen und verdecken sie fast komplett. Um diesen Unterschied hervorgerufen durch die erhöhte Ratenfrequenz genauer untersuchen zu können, soll der relative Unterschied zu p geplottet werden.

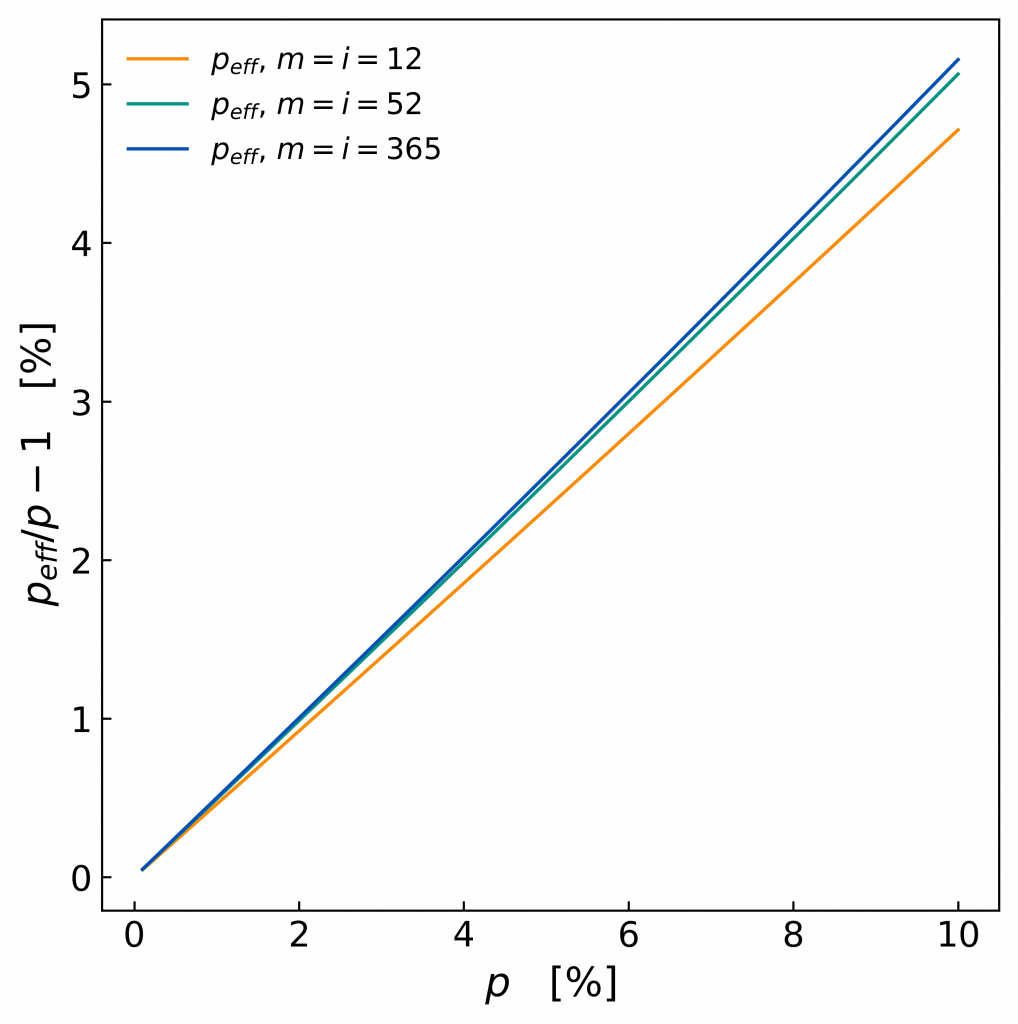
Hier zeigt sich, dass p_eff umso größer ist, je höher die Ratenfrequenz ist und dass der Unterschied größer ist, wenn p groß ist.

Fazit

Zusammengenommen kann man aus diesen Abbildungen ziehen, dass der effektive Jahreszinssatz p_eff umso größer ist, je höher der nominale Jahreszinssatz p ist. Der dadurch bedingte Zineszinseffekt wird also für eine höhere Zinslast sorgen, umso höher der nominale Jahreszinssatz p ist. Aus Kreditnehmersicht ist es also nur zu begrüßen, einen möglichst niedrigen Nominalzinssatz (p.a.) erhalten zu können.

Darüber hinaus macht es auch einen Unterschied, wie oft eine Kreditrate gefordert wird, denn je niederiger die Ratenfrequenz, desto niedriger der effektive Jahreszinssatz p_eff.